A synthetic image is the result of convolving the 2D target scene with the 2D PSF of the system. In practice, this convolution is only evaluated at the centre of each pixel in the output image; see this previous post for a more detailed explanation of the algorithm. That post covers the method used to simulate an aberration-free ideal lens, often called a diffraction-limited lens, combined with the photosite aperture of the sensor. The Airy pattern which models the effects of diffraction is readily modelled using a jinc(x) function, but if we want to add in the effects of defocus and spherical aberration things become a little bit harder.
I can recommend Jack Hogan's excellent article on the topic, which describes the analytical form of a PSF that combines diffraction, defocus and spherical aberration. I repeat a version of this equation here with the normalization constant omitted:
The PSF(r) equation contains two parameters that relate to radial distances: r, which denotes the normalized distance from the centre of the PSF, and ρ, which denotes a normalized radial distance across the exit pupil of the lens. Unfortunately we have to integrate out the ρ parameter to obtain our estimate of the PSF at each radial distance r that we wish to sample the PSF. Figure 1 below illustrates our sampled PSF as a function of r (the PSF is shown mirrored around r=0 for aesthetic reasons). Keep in mind that for a radially symmetric PSF, r is in the range [0, ∞). For practical purposes we have to truncate r at some point, but this point is somewhere around 120 λN units (λ is the wavelength, N is the f-number of the lens aperture).
 |
| Figure 1: Sampled PSF of the combined effect of circular aperture diffraction and spherical aberration. |
Integrating oscillating functions is hard
Numerical integration is hard, like eating a bag of pine cones, but that is peanuts compared to numerical integration of oscillating functions. Where does all this oscillation come from? Well, that Bessel function of the first kind (of order 0), J0, looks like this when r=20 (and λN = 1):
 |
| Figure 2: Bessel J0 when r=20 |
 |
| Figure 3: Notice how the area of the negative rectangles do not appear to cancel the area of the positive rectangles very well. |
Fortunately there is a very simple solution to this problem: we just split our function into intervals between the zero crossings of f(), integrate each interval separately, and add up the partial integrals. This strategy is excellent if we know where the zero crossings are.
And our luck appears to be holding, because the problem of finding the zero crossings of the Bessel J0 function has already been solved [1]. The algorithm is fairly simple: we know the location of the first two roots of J0, they are at x1=2.404826 and x2=5.520078, and subsequent roots can be estimated as xi = xi-1 + (xi-1 - xi-2), for i >= 3. We can refine those roots using a Newton-Raphson iteration, where xi,j = xi,j-1 + J0(xi,j-1)/J1(xi,j-1), and J1 is the Bessel function of the first kind of order 1. We also know that if our maximum r is 120, then we expect 120 roots, and we just have to apply our numerical integration routine to each interval defined by [xi-1, xi] (plus the endpoints 0 and 120, of course).
But we are not quite there yet. Note that our aberration function γ(ρ) is a complex exponential function. If either the W020 or the W040 coefficient is non-zero, then our J0 function is multiplied by another oscillatory function, but fortunately the oscillations are a function of ρ, and not r, so this does not introduce enough oscillation to cause major problems for realistic values, since W020 < 20 and W040 < 20. This is not the only challenge that γ(ρ) introduces, though. Although our final PSF is a real-valued function, the entire integrand is complex, and care must be taken to only apply the modulus operator to the final result. This implies that we must keep all the partial integrals of our [xi-1, xi] intervals as a complex numbers, but it also requires the actual numerical integration routine to operate on complex numbers. Which brings us to the selection of a suitable numerical integration routine ....
Candidate numerical integration routines
The simplest usable integration routine that I know of is the adaptive variant of Simpson's rule, but this only works well if your integrand is sufficiently smooth, and your subdivision threshold is chosen carefully. The adaptive Simpson algorithm is exceedingly simple to implement, so that was the first thing I tried. Why did I want to use my own implementation? Why not use something like Boost or GSL to perform the integration?
Well, the primary reason is that I dislike adding dependencies to MTF Mapper unless it is absolutely necessary. There is nothing worse, in my experience, than trying to build some piece of open-source code from source, only to spend hours trying to get just the right version of all the dependencies. Pulling in either Boost or GSL as a dependency just because I want to use a single integration routine is just not acceptable. Anyway, why would I pass up the opportunity to learn more about numerical integration? (Ok, so I admit, this is the real reason. I learn most when I implement things myself.)
So I gave the adaptive Simpson algorithm a try, and it seemed to work well enough when I kept r < 20, thus avoiding the more oscillatory parts of the integrand. It was pretty slow, just like the literature predicted [2]. I decided that I will look for a better algorithm, but one that is still relatively simple to implement. This led me to TOMS468, and a routine called QSUBA. This FORTRAN77 implementation employs an adaptive version of Gauss-Kronrod integration. Very briefly, one of the main differences between Simpson's rule and Gaussian quadrature (quadrature = archaic name for integration) is that the former approximates the integrand with a quadratic polynomial with regularly-spaced samples, whereas the latter can approximate the integrand as the product of a weighting function and a higher-order polynomial (with custom spacing). The Kronrod extension is a clever method of choosing our sample spacing that allows us to re-use previous values while performing adaptive integration.
Much to my surprise, I could translate the TOMS468 FORTRAN77 code to C code using f2c, and it worked out of the box. It took quite a bit longer to port that initial C code to something that resembles good C++ code; all the spaghetti GOTO statements in the FORTRAN77 was faithfully preserved in the f2c output. I also had to extend the algorithm a little to support complex integrands.
 |
| Figure 4: QSUBA integration without roots (top), and with roots (bottom). Note the logarithmic y-axis scale |
 |
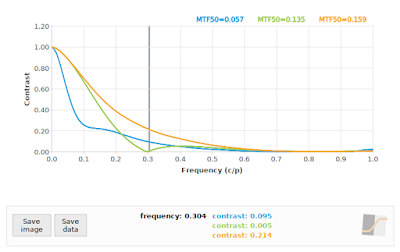
| Figure 5: MTF derived from the two PSFs shown in Figure 4. |
Rendering the image
After having obtained a decent-looking PSF as explained above, the next step is to construct a cumulative density function (CDF) using the PSF, but this time we take into account that the real PSF is 2D. We can still do this with a 1D CDF, but at radial distance r we have to correct the probability proportionally to the area of a disc of radius r. The method is described in detail in the section titled "Importance sampling and the Airy disc" in this post. The next step is to generate 2D sampling locations drawn from the CDF, which effectively places sampling locations with a density proportional to the intensity of the 2D PSF.
If we are simulating just the lens part, we just calculate what fraction of our sampling locations are inside the target polygon geometry (e.g., our black rectangles), and shade our output pixel accordingly. To add in the effect of the sensor's photosite aperture, which is essentially an additional convolution of our PSF with a square the size of our photosites if we assume a 100% fill factor, we just replace the point-in-target-polygon test with an intersect-photosite-aperture-polygon-with-target-polygon step. This trick means that we do not have to resort to any approximations (e.g., discrete convolutions) to simulate the sensor side of our system PSF. Now for a few examples, as promised.
 |
| Figure 6: MTF curves of simulated aberrations. The orange curve is f/5.6 with W040 = 0.75 (i.e., significant spherical aberration). The blue curve is f/5.6 with W040 = 2 (i.e., extreme spherical aberration). The green curve is f/5.6 with no spherical aberration, but W020 = 1 (i.e., a lot of defocus). |
Before I show you the rendered images, take a look at Figure 6 to see what the MTF curves of the simulated images look like. First up, the orange curve with W040 = 0.75. This curve sags a little between 0.1 and 0.4 cycles/pixel, compared to the same lens without the simulated spherical aberration, but otherwise it still looks relatively normal. Figure 7 illustrates what a simulated image with such an MTF curve looks like.
 |
| Figure 7: Simulated lens at f/5.6 with W040 = 0.75, corresponding to the orange curve in Figure 6. Looks OK, if a little soft. (remember to click on the image for a 100% view) |
The blue curve (in Figure 6) represents severe spherical aberration with W040 = 2, also rendered at f/5.6. Notice how the shape of the blue curve looks very different from what we typically see on (most?) real lenses, where the designers presumably do their best to keep the spherical aberrations from reaching this magnitude. The other interesting thing about the blue curve is that contrast drops rapidly in the range 0 to 0.1 cycles/pixel, but despite the sudden drop we then have a more gradual decrease in contrast. This simulated lens gives us Figure 8.
 |
| Figure 8: Simulated lens at f/5.6 with W040 = 2, corresponding to the blue curve in Figure 6. This image has the typical glow that I associate with spherical aberration. |
Figure 9 illustrates a simulated scene corresponding to the green curve in Figure 6, representing significant defocus with W020 = 1, but no spherical aberration with W040 = 0. It also exhibits a new MTF curve shape that requires some explanation. It only appears as if the curve "bounces" at about 0.3 cycles per pixel; what is happening is that the OTF undergoes phase inversion between, say, 0.3 and 0.6 cycles per pixel, but the because the MTF is the modulus of the OTF we see this rectified version of the OTF (see Jack Hogan's article on defocus for an illustration of the OTF under defocus).
 |
| Figure 9: Simulated lens at f/5.6 with W020 = 1.0, corresponding to the green MTF curve in Figure 6. If you look very closely at 100% magnification (click on the image), you might just see some detail between the "2" and the "1" marks on the trumpet. This corresponds to the frequencies around 0.4 c/p, i.e., just after the bounce. |
 |
| Figure 10: Simulated lens at f/5.6 with W020 = 2.0. This image looks rather out of focus, as one would expect, but notice how the contrast fades near the "7" mark on the trumpet, but then recovers somewhat between the "6" and "3" marks. This corresponds to the "bounce" near 0.3 cycles/pix we saw in the MTF curve. Look closely, and you will see the black and white stripes have been reversed between the "6" and "3" marks. |
Sample usage
To reproduce the simulated images shown above, first grab an instance of the "pinch.txt" test chart geometry here. Then you can render the scenes using the following commands:
mtf_generate_rectangle.exe --target-poly pinch.txt -p wavefront-box --aperture 5.6 --w040 2.0 -n 0.0 -o pinch_example.png
This should produce an 8-bit sRGB PNG image called pinch_example.png with significant spherical aberration (the --w040 parameter). You can use the --w020 parameter to add defocus to the simulation. Note that both these aberration coefficient arguments only take effect if you use either the wavefront-box or wavefront PSF models (as argument to the -p option); in general I recommend using the wavefront-box PSF, unless you specifically want to exclude the sensor photosite aperture component for some reason.
These new PSF models are available in MTF Mapper versions 0.7.4 and up.
Caveats
I am satisfied that the rendering algorithm implemented in mtf_generate_rectangle produces the correct PSF, and eventually MTF, for simulated systems with defocus and/or spherical aberration. What I have not yet confirmed to my own satisfaction is that the magnitude of the aberrations W020 and W040, currently expressed as multiples of the wavelength (λ), does indeed effect an aberration with a physically-correct magnitude. In other words, see them as unitless parameters that control the magnitude of the aberrations.
I hope to verify that the magnitude is physically correct at some point in the future.
If you simulate highly aberrated lenses, such as f/5.6 with W020 = 2, and measure a slanted-edge in the resulting image, you may notice that MTF Mapper does not reproduce the sharp "bounces" in the SFR curve quite as nicely as shown in Figure 6. You can add the "--nosmoothing" option to the Arguments field in the Preferences dialog to make those "bounces" more crisp, but this is only recommended if your image contains very low levels of image noise.
Another somewhat unexpected property of the W020 and W040 aberration coefficients is that the magnitude of their effect interacts strongly with the simulated f-number of the lens. In other words, simulating W020 = 0.5 at f/16 looks a lot more out-of-focus than W020 = 0.5 at f/2.8. This is because the W020 and W040 coefficients are specified as a displacement (along the axis of the lens) at the edge of the exit pupil of the lens, meaning that their angular impact depends strongly on the diameter of the exit pupil. Following Jack's article, the diameter of the defocus disc at the sensor plane scales as 8N λ W020 (translated to my convention for W020 and W040). Thus, if we want the same defocus disc diameter at f/2.8 that we saw at f/16 with W020 = 0.5, then we should choose W020 = 16/2.8 * 0.5 = 2.857. If I compare simulated images at f/2.8 with W020 = 2.857 to those at f/16 with W020 = 0.5, then it at least looks as if both images have a similar amount of blur, but obviously the f/16 image will lack a lot of the higher-frequency details outright.
Hold on a minute ...
The astute reader might have noticed something odd about the equation given for PSF(r) in the introduction. If we set W020 = 0, W040 = 0, N = 1 and λ = 1, then γ(ρ) is real-valued and equal to 1.0. This reduces the integral to
But without any defocus or spherical aberration, we should obtain the Airy pattern PSF that we have used in the past, i.e, we should get
References
- S.K. Lucas and H.A. Stone, "Evaluating infinite integrals involving Bessel functions of arbitrary order", Journal of Computational and Applied Mathematics, 64:217-231, 1995.
- I. Robinson, "A comparison of numerical integration programs", Journal of Computational and Applied Mathematics, 5(3):207-223, 1979.
- R. Piessens, "The Hankel transform", in The transforms and applications handbook, CRC press, 2000. (PDF here)
