A brief overview of lens distortion correction

Before I post an article on the details of MTF Mapper's automatic lens distortion correction features, I would like to describe in some detail the lens distortion model adopted by MTF Mapper.

The basics

Radial lens distortion is pretty much as the name suggests: the lens distorts the apparent radial position of an imaged point, relative to its ideal position predicted by the simple pinhole model. The pinhole model tells us that the position of a point in the scene, P(x, y, z) [assumed to be in the camera reference frame], is projected onto the image plane at position p(x, y) as governed by the focal length f, such that

    p_x = (P_x - C_x) * f/(P_z - C_z)

    p_y = (P_y - C_y) * f/(P_z - C_z)

where C(x, y, z) represents the centre of projection of the lens (i.e., the apex of the imaging cone).

We can express the point p(x, y) in polar coordinates as p(r, theta), where r² = p_x² + p_y²; the angle theta is dropped, since we assume that the radial distortion is symmetrical around the optical axis.

Given this description of the pinhole part of the camera model, we can then model the observed radial position r_d as 

    r_d = r_u * F(r_u)

where the function F() is some function that describes the distortion, and r_u is the undistorted radial position, which we simply called "r" above in the pinhole model.

Popular choices of F() include:

• Polynomial model (simplified version of Brown's model), with
  F(r_u) = 1 + k₁ * r_u² + k₂ * r_u⁴
• Division model (extended version of Fitzgibbon's model), with
  F(r_u) = 1 / (1 + k₁ * r_u² + k₂ * r_u⁴)

Note that these models are really just simple approximations to the true radial distortion function of the lens; these simple models persist because they appear to be sufficiently good approximations for practical use.

I happen to prefer the division model, mostly because it is reported in the literature to perform slightly better than the polynomial model [1, 2].

Some examples of radial distortion

Now for some obligatory images of grid lines to illustrate the common types of radial lens distortion we are likely to encounter. First off, the undistorted grid:

Figure 1: What the grid should look like on a pinhole camera

Add some barrel distortion (k₁ = -0.3, k₂ = 0 using division model) to obtain this:

Figure 2: Barrel distortion, although I think "Surface of an inflated balloon distortion" would be more apt.

Note how the outer corners of our grid lines appear at positions closer to the centre than we saw in the undistorted grid. We can instead move those corners further outwards from where they were in the undistorted grid to obtain pincushion distortion (k₁ = 0.3, k₂ = 0 using division model):

Figure 3: Pincushion distortion, although I would prefer "inaccurate illustration of gravitationally-induced distortion in space-time".

If we combine these two main distortion types, we obtain moustache distortion (k₁ = -1.0, k₂ = 1.1 using division model):

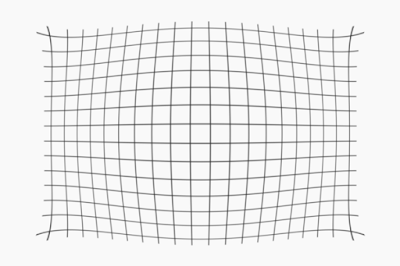Figure 4: Moustache distortion.

We can swap the order of the barrel and pincushion components to obtain another type of moustache distortion, although I do not know if any extant lenses actually exhibit this combination (k₁ = 0.5, k₂ = -0.5 using division model):

Figure 5: Alternative (inverted?) moustache distortion.

Quantifying distortion

Other than using the k₁ and k₂ parameters (which might be a bit hardcore for public consumption), how would we summarize both the type and the magnitude of a lens' radial distortion? It appears that this is more of a rhetorical question than we would like it to be. There are several metrics currently in use, most of them unsatisfying in some respect or another.

One of the most widely used metrics is SMIA "TV distortion", which expresses distortion as a percentage in accordance with the following diagram:

Figure 6: Slightly simplified SMIA TV distortion

The SMIA TV distortion metric is just 100*(A - B)/B. If the value is negative you have barrel distortion, and positive values imply pincushion distortion. If you have moustache distortion like shown in Figures 4 and 5, then you could very likely obtain a value of 0% distortion. Whoops!

I only show SMIA TV distortion here to make a concrete link to the k₁ parameter, and to highlight that SMIA TV distortion is not useful in the face of moustache distortion.

Using the division model

There is one subtlety that is worth pondering a while: are we modelling the forward distortion, i.e, the distortion model maps our undistorted pinhole projected points to their distorted projected points, or are we modelling the reverse mapping, i.e., we model the correction required to map the distorted projected points to their undistorted pinhole projected points?

The important point to note is that neither the polynomial model, nor the division model, compels us to choose a specific direction, and both models can successfully be applied in either direction by simply swapping r_d and r_u in the equations above. I can think of two practical implications of choosing a specific direction:

1. If we choose the forward direction (such as presented above in "The basics") where r_d = r_u * F(r_u), then we must have a way of inverting the distortion if we want to correct an actual distorted image as received from the camera. If we undistort an entire image, then we would prefer to have an efficient implementation of the reverse mapping, i.e., we require an efficient inverse function F^-1() so that we may calculate F^-1(r_d) = r_d/r_u. In this form it is not immediately clear that we can find a closed-form solution to the reverse mapping, and we may have to resort to an iterative method to effect the reverse mapping. Depending on how we plan to obtain our distortion coefficients k₁ and k₂, it may be that the forward distortion approach could be far more computationally costly than the reverse distortion approach. To summarize: inverting the distortion model for each pixel in the image can be costly.
2. The process of estimating k₁ and k₂ typically involves a non-linear optimization process, which can be computationally costly if we have to compute the reverse mapping on a large number of points during each iteration of the optimization algorithm. I have a strong aversion to using an iterative approximation method inside of an iterative optimization process, since this is almost certainly going to be rather slow. To summarize: inverting the distortion model during non-linear optimization of k₁ and k₂ can be costly.

Just how costly is it to compute the undistorted points given the distorted points and a forward distortion model?

• Polynomial model:
  r_d = r_u * (1 + k₁ * r_u² + k₂ * r_u⁴), or after collecting terms,
  r_u + r_u * k₁ * r_u² + r_u * k₂ * r_u⁴ - r_d = 0
  k₁ * r_u³ + k₂ * r_u⁵ + r_u - r_d = 0
  Since we are given r_d, we can compute potential solutions for r_u by finding the roots of a 5th-order polynomial.
• Division model:
  r_d = r_u / (1 + k₁ * r_u² + k₂ * r_u⁴), or
  r_d * k₁ * r_u² + r_d * k₂ * r_u⁴ - r_u + r_d = 0
  This looks similar to the polynomial model, but at least we only have to find the roots of a 4th-order polynomial, which we can do using Ferrari's formula because the r_u³ term has already been deflated.

In both cases we have to find the all the roots, including the complex ones, and then choose the appropriate real root to obtain r_u given r_d (I assume here that the distortion is invertible, which we can enforce in practice by constraining k₁ and k₂ as proposed by Santana-Cedres et al. [3]).
Alternatively, we could try a fixed-point iteration scheme, i.e., initially guess that r_u = r_d, substitute this into the equation r_u  = r_d / F(r_u) to obtain a new estimate of r_u, rinse and repeat until convergence (this is what OpenCV does). Both of these approaches are far too computationally demanding to calculate for every pixel in the image, so it would appear that we would be better off by estimating the reverse distortion model.

But there is a trick that we can employ to speed up the process considerably. First, we note that our normalized distorted radial values are in the range [0, 1], if we normalize such that the corner points of our image have r = 1, and the image centre has r = 0. Because the interval is closed, it is straightforward to construct a look-up table to give us r_u for a given r_d, using, for example, the root-finding solutions above. If we construct our look-up table such that r_d is sampled with a uniform step length, then we can use a pre-computed quadratic fit to interpolate through the closest three r_d values to obtain a very accurate estimate of r_u. The combination of a look-up table plus quadratic interpolation is almost as fast as evaluating the forward distortion equation. The only limitation to the look-up table approach, though, is that we have to recompute the table whenever k₁ or k₂ changes, meaning that the look-up table method is perfect for undistorting an entire image for a given k₁ and k₂, but probably too expensive to use during the optimization task to find k₁ and k₂.

So this is exactly what MTF Mapper does: the forward distortion model is adopted so that the optimization of k₁ and k₂ is efficient, with a look-up table + quadratic interpolation implementation for undistorting the entire image.

Some further observations on the models

If you stare at the equation for the inversion of the division model for a while, you will see that 

    r_d * k₁ * r_u² + r_d * k₂ * r_u⁴ - r_u + r_d = 0

neatly reduces to

    r_d * k₁ * r_u²  - r_u + r_d = 0

if we assume that k₂ = 0. This greatly simplifies the root-finding process, since we can use the well-known quadratic formula, or at least, the numerically stable version of it. This is such a tempting simplification of the problem that many authors [1, 2] claim that a division model with only a single k₁ parameter is entirely adequate for modeling radial distortion in lenses.

That, however, is demonstrably false in the case of moustache distortion, which requires a local extremum or inflection point in the radial distortion function. For example, the distortion function that produces Figure 4 above looks like this:

Figure 7: The distortion function F() corresponding to Figure 4.

It is clear that the division model with k₂ = 0 cannot simultaneously produce the local minimum observed at the left (r_d = 0) and the local maximum to the right (r_d ~ 0.65).

Similar observations apply to the polynomial model, i.e., we require k₂ ≠ 0 to model moustache distortion.

Wrapping up

I think that covers the basics of radial distortion modelling. In a future article I will demonstrate how one would go about determining the parameters k₁ and k₂ from a sample image.

References

1. Fitzgibbon, A.W., Simultaneous linear estimation of multiple view geometry and lens distortion, Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2001.
2. Wu, F, Wei, H, Wang, X, Correction of image radial distortion based on division model, SPIE Optical Engineering, 56(1), 2017.
3. Santana-Cedres, D, et al., Invertibility and estimation of two-parameter polynomial and division lens distortion models, SIAM Journal on Imaging Sciences, 8(3):1574-1606, 2015.