A brief overview of lens distortion correction

Before I post an article on the details of MTF Mapper's automatic lens distortion correction features, I would like to describe in some detail the lens distortion model adopted by MTF Mapper.

The basics

Radial lens distortion is pretty much as the name suggests: the lens distorts the apparent radial position of an imaged point, relative to its ideal position predicted by the simple pinhole model. The pinhole model tells us that the position of a point in the scene, P(x, y, z) [assumed to be in the camera reference frame], is projected onto the image plane at position p(x, y) as governed by the focal length f, such that

    p_x = (P_x - C_x) * f/(P_z - C_z)

    p_y = (P_y - C_y) * f/(P_z - C_z)

where C(x, y, z) represents the centre of projection of the lens (i.e., the apex of the imaging cone).

We can express the point p(x, y) in polar coordinates as p(r, theta), where r² = p_x² + p_y²; the angle theta is dropped, since we assume that the radial distortion is symmetrical around the optical axis.

Given this description of the pinhole part of the camera model, we can then model the observed radial position r_d as 

    r_d = r_u * F(r_u)

where the function F() is some function that describes the distortion, and r_u is the undistorted radial position, which we simply called "r" above in the pinhole model.

Popular choices of F() include:

• Polynomial model (simplified version of Brown's model), with
  F(r_u) = 1 + k₁ * r_u² + k₂ * r_u⁴
• Division model (extended version of Fitzgibbon's model), with
  F(r_u) = 1 / (1 + k₁ * r_u² + k₂ * r_u⁴)

Note that these models are really just simple approximations to the true radial distortion function of the lens; these simple models persist because they appear to be sufficiently good approximations for practical use.

I happen to prefer the division model, mostly because it is reported in the literature to perform slightly better than the polynomial model [1, 2].

Some examples of radial distortion

Now for some obligatory images of grid lines to illustrate the common types of radial lens distortion we are likely to encounter. First off, the undistorted grid:

Figure 1: What the grid should look like on a pinhole camera

Add some barrel distortion (k₁ = -0.3, k₂ = 0 using division model) to obtain this:

Figure 2: Barrel distortion, although I think "Surface of an inflated balloon distortion" would be more apt.

Note how the outer corners of our grid lines appear at positions closer to the centre than we saw in the undistorted grid. We can instead move those corners further outwards from where they were in the undistorted grid to obtain pincushion distortion (k₁ = 0.3, k₂ = 0 using division model):

Figure 3: Pincushion distortion, although I would prefer "inaccurate illustration of gravitationally-induced distortion in space-time".

If we combine these two main distortion types, we obtain moustache distortion (k₁ = -1.0, k₂ = 1.1 using division model):

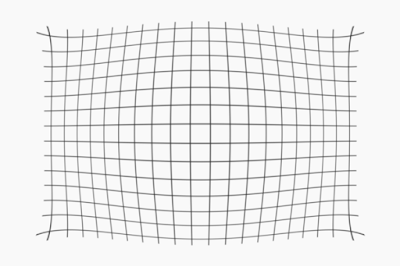Figure 4: Moustache distortion.

We can swap the order of the barrel and pincushion components to obtain another type of moustache distortion, although I do not know if any extant lenses actually exhibit this combination (k₁ = 0.5, k₂ = -0.5 using division model):

Figure 5: Alternative (inverted?) moustache distortion.

Quantifying distortion

Other than using the k₁ and k₂ parameters (which might be a bit hardcore for public consumption), how would we summarize both the type and the magnitude of a lens' radial distortion? It appears that this is more of a rhetorical question than we would like it to be. There are several metrics currently in use, most of them unsatisfying in some respect or another.

One of the most widely used metrics is SMIA "TV distortion", which expresses distortion as a percentage in accordance with the following diagram:

Figure 6: Slightly simplified SMIA TV distortion

The SMIA TV distortion metric is just 100*(A - B)/B. If the value is negative you have barrel distortion, and positive values imply pincushion distortion. If you have moustache distortion like shown in Figures 4 and 5, then you could very likely obtain a value of 0% distortion. Whoops!

I only show SMIA TV distortion here to make a concrete link to the k₁ parameter, and to highlight that SMIA TV distortion is not useful in the face of moustache distortion.

Using the division model

There is one subtlety that is worth pondering a while: are we modelling the forward distortion, i.e, the distortion model maps our undistorted pinhole projected points to their distorted projected points, or are we modelling the reverse mapping, i.e., we model the correction required to map the distorted projected points to their undistorted pinhole projected points?

The important point to note is that neither the polynomial model, nor the division model, compels us to choose a specific direction, and both models can successfully be applied in either direction by simply swapping r_d and r_u in the equations above. I can think of two practical implications of choosing a specific direction:

1. If we choose the forward direction (such as presented above in "The basics") where r_d = r_u * F(r_u), then we must have a way of inverting the distortion if we want to correct an actual distorted image as received from the camera. If we undistort an entire image, then we would prefer to have an efficient implementation of the reverse mapping, i.e., we require an efficient inverse function F^-1() so that we may calculate F^-1(r_d) = r_d/r_u. In this form it is not immediately clear that we can find a closed-form solution to the reverse mapping, and we may have to resort to an iterative method to effect the reverse mapping. Depending on how we plan to obtain our distortion coefficients k₁ and k₂, it may be that the forward distortion approach could be far more computationally costly than the reverse distortion approach. To summarize: inverting the distortion model for each pixel in the image can be costly.
2. The process of estimating k₁ and k₂ typically involves a non-linear optimization process, which can be computationally costly if we have to compute the reverse mapping on a large number of points during each iteration of the optimization algorithm. I have a strong aversion to using an iterative approximation method inside of an iterative optimization process, since this is almost certainly going to be rather slow. To summarize: inverting the distortion model during non-linear optimization of k₁ and k₂ can be costly.

Just how costly is it to compute the undistorted points given the distorted points and a forward distortion model?

• Polynomial model:
  r_d = r_u * (1 + k₁ * r_u² + k₂ * r_u⁴), or after collecting terms,
  r_u + r_u * k₁ * r_u² + r_u * k₂ * r_u⁴ - r_d = 0
  k₁ * r_u³ + k₂ * r_u⁵ + r_u - r_d = 0
  Since we are given r_d, we can compute potential solutions for r_u by finding the roots of a 5th-order polynomial.
• Division model:
  r_d = r_u / (1 + k₁ * r_u² + k₂ * r_u⁴), or
  r_d * k₁ * r_u² + r_d * k₂ * r_u⁴ - r_u + r_d = 0
  This looks similar to the polynomial model, but at least we only have to find the roots of a 4th-order polynomial, which we can do using Ferrari's formula because the r_u³ term has already been deflated.

In both cases we have to find the all the roots, including the complex ones, and then choose the appropriate real root to obtain r_u given r_d (I assume here that the distortion is invertible, which we can enforce in practice by constraining k₁ and k₂ as proposed by Santana-Cedres et al. [3]).
Alternatively, we could try a fixed-point iteration scheme, i.e., initially guess that r_u = r_d, substitute this into the equation r_u  = r_d / F(r_u) to obtain a new estimate of r_u, rinse and repeat until convergence (this is what OpenCV does). Both of these approaches are far too computationally demanding to calculate for every pixel in the image, so it would appear that we would be better off by estimating the reverse distortion model.

But there is a trick that we can employ to speed up the process considerably. First, we note that our normalized distorted radial values are in the range [0, 1], if we normalize such that the corner points of our image have r = 1, and the image centre has r = 0. Because the interval is closed, it is straightforward to construct a look-up table to give us r_u for a given r_d, using, for example, the root-finding solutions above. If we construct our look-up table such that r_d is sampled with a uniform step length, then we can use a pre-computed quadratic fit to interpolate through the closest three r_d values to obtain a very accurate estimate of r_u. The combination of a look-up table plus quadratic interpolation is almost as fast as evaluating the forward distortion equation. The only limitation to the look-up table approach, though, is that we have to recompute the table whenever k₁ or k₂ changes, meaning that the look-up table method is perfect for undistorting an entire image for a given k₁ and k₂, but probably too expensive to use during the optimization task to find k₁ and k₂.

So this is exactly what MTF Mapper does: the forward distortion model is adopted so that the optimization of k₁ and k₂ is efficient, with a look-up table + quadratic interpolation implementation for undistorting the entire image.

Some further observations on the models

If you stare at the equation for the inversion of the division model for a while, you will see that 

    r_d * k₁ * r_u² + r_d * k₂ * r_u⁴ - r_u + r_d = 0

neatly reduces to

    r_d * k₁ * r_u²  - r_u + r_d = 0

if we assume that k₂ = 0. This greatly simplifies the root-finding process, since we can use the well-known quadratic formula, or at least, the numerically stable version of it. This is such a tempting simplification of the problem that many authors [1, 2] claim that a division model with only a single k₁ parameter is entirely adequate for modeling radial distortion in lenses.

That, however, is demonstrably false in the case of moustache distortion, which requires a local extremum or inflection point in the radial distortion function. For example, the distortion function that produces Figure 4 above looks like this:

Figure 7: The distortion function F() corresponding to Figure 4.

It is clear that the division model with k₂ = 0 cannot simultaneously produce the local minimum observed at the left (r_d = 0) and the local maximum to the right (r_d ~ 0.65).

Similar observations apply to the polynomial model, i.e., we require k₂ ≠ 0 to model moustache distortion.

Wrapping up

I think that covers the basics of radial distortion modelling. In a future article I will demonstrate how one would go about determining the parameters k₁ and k₂ from a sample image.

References

1. Fitzgibbon, A.W., Simultaneous linear estimation of multiple view geometry and lens distortion, Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2001.
2. Wu, F, Wei, H, Wang, X, Correction of image radial distortion based on division model, SPIE Optical Engineering, 56(1), 2017.
3. Santana-Cedres, D, et al., Invertibility and estimation of two-parameter polynomial and division lens distortion models, SIAM Journal on Imaging Sciences, 8(3):1574-1606, 2015.

Image interpolation: Fighting the fade, part 1

Over the last six months or so I kept on bumping into a particularly vexing problem related to image interpolation: the contrast in an interpolated image drops to zero in the worst case of interpolating at an exact half-pixel shift relative to the original image.

Consider the case where you are trying to co-register (align) two images, such as two images captured by the same camera, but with a small translation of the camera between the two shots. If we translate the camera purely in the horizontal direction, then the shift between the two images will be h pixels, where h can be any real number. The integer part of h will not cause us any trouble for reasonable values of h, such that the two images still overlap, of course. The trouble really lies in the fractional part of h, since this forces us to interpolate pixel values from the moving image if we want it to line up correctly with the fixed image.

The worst case scenario, as mentioned above, is if the fractional part of h is exactly 0.5 pixels, since this implies that the value of a pixel in the interpolated moving image will be the mean of the two closest pixels from the original moving image. Figure 1 illustrates what such an interpolated moving image will look like for a half-pixel shift; the edges are annotated with their MTF50 values.

Figure 1: Scaled (Nearest Neighbour interpolation) view of an interpolated moving image that experienced a half-pixel shift. The numbers are the measured MTF50 values, in cycles/pixel.

Looking closely at the vertical edges of the gray square, we can see that there are some visible interpolation artifacts manifesting as overshoot and undershoot. This image was interpolated using OMOMS cubic spline interpolation [2], which is best method that I am aware of. Linear interpolation would produce much more blurring (but no overshoot/undershoot). And of course we see a marked drop in MTF50 on the vertical edges!

At any rate, the MTF curves for the edges are illustrated in Figure 2. The blue curve corresponds to the horizontal edge (i.e., the direction that experienced no interpolation), and the orange curve corresponds to the vertical edge (an 0.5-pixel horizontal shift interpolation). The green curve was obtained from another simulation where the moving image was shifted by 0.25 pixels.

Figure 2: MTF curves of interpolated moving images corresponding to fractional horizontal shifts of zero (blue), 0.25 pixels (green), and 0.5 pixels (orange).

Certainly the most striking feature of the orange curve is how the contrast drops to exactly zero at the Nyquist frequency (0.5 cycles/pixel). The smaller 0.25-pixel shift (green curve) shows a dip in contrast around Nyquist, but this would probably not be noticeable in most images.

In Figure 3 we can see that this loss of contrast around Nyquist follows a smooth progression as we approach a fractional shift of 0.5 pixels.

Figure 3: MTF curves of interpolated moving images corresponding to fractional horizontal shifts of 0.25 pixels (blue), 0.333 pixels (green), and 0.425 pixels (orange).

The conclusion from this experiment is that we really want to avoid interpolating an image with a fractional shift of 0.5 pixels (in either/both horizontal and vertical directions), since this will produce a very noticeable loss of contrast at higher frequencies, i.e., we will lose all the fine details in the interpolated image.

Radial distortion lens correction

An applied example of where this interpolation problem crops up is when we apply a radial distortion correction model to improve the geometry of images captured by a lens exhibiting some distortion (think barrel or pincushion distortion). I aim to write a more thorough article on this topic soon, but for now it suffices to say that our radial distortion correction model specifies for each pixel (x, y) in our corrected image where we have to go and sample the distorted image.

I prefer to use the division model [1], which implies that for a pixel (x, y) in the corrected image, we go and sample the pixel at

    x' = (x - x_c) / (1 + k₁r² + k₂r⁴) + x_c

where

    r = sqrt((x - x_c)² + (y - y_c)²)
and (x_c, y_c) denotes the centre of distortion (which could be the centre of the image, for example).

The value of y' is calculated the same way. The actual distortion correction is then simply a matter of visiting each pixel (x, y) in our undistorted image, and setting its value to the interpolated value extracted from (x', y') in the distorted image.

The important part to remember here is that the value (x', y') can assume any fractional pixel value, including the dreaded half-pixel shift.

An example of mild pincushion distortion

In order to illustrate the effects of radial distortion correction, I thought it best to start with synthetic images with known properties. Figure 4 illustrates a 100% crop near the top-left corner of the reference image, i.e., what we would have obtained if the lens did not have any distortion.

Figure 4: The pure, undistorted reference image. Note that the closely-spaced black lines blur into gray bars because of the simulated Gaussian Point Spread Function (PSF) with an MTF50 of 0.35 c/p. If you squint hard enough, you can see some traces of the original black bars. Rendered at 400% size with nearest-neighbour upscaling. (click for 100% view)

I simulated a very mild pincushion distortion with k₁ = 0.025 and k₂ = 0, which produces an SMIA lens distortion figure of about -1.62%. This distortion was applied to the polygon geometry, which was again rendered with a Gaussian PSF with an MTF50 of 0.35 c/p. The result is shown in Figure 5. Keep in mind that you cannot really see the pincusion distortion at this scale, since we are only looking at the top-left corner of a much larger image.

Figure 5: Similar to Figure 4, but with about 1.62% pincushion distortion applied to the polygon geometry. Rendered at 400% size with nearest-neighbour upscaling. (click for 100% view)

We can see the first signs of trouble in Figure 5: Notice how the black/white bars appear to "fade out" at regular intervals. The straight lines of Figure 4 are no longer perfectly straight, nor are they aligned with the image rows and columns. The lines thus cross from one row (or column) to the next, and the gray patches correspond to the regions where the lines fell halfway between two rows (or columns), leading to the apparent loss of contrast.

It is important to understand at this point that the fading in Figure 5 is not a processing artifact; this is exactly what would happen if you were to photograph similar thin bars that are not aligned with the image rows/columns.

Finally, we arrive at the radial distortion correction phase. Figure 6 illustrates what the corrected image would look like if we used standard cubic interpolation to resample the image.

Figure 6: The undistorted version of Figure 5. Resampling was performed using standard cubic interpolation. Rendered at 400% size with nearest-neighbour upscaling. (click for 100% view).

We see some additional fading that appears in Figure 6. If you flick between Figures 5 and 6 (after clicking for 100% view) you will notice that an extra set of fading patches appear in between the original fading patches. These extra fades are the manifestation of the phenomenon illustrated in Figure 2: the contrast drops to zero as the interpolation sample position approaches a fractional pixel offset of 0.5. The interesting thing about these additional fades is that they are not recoverable using sharpening --- once the contrast reaches zero, no amount of sharpening will be able to recover it.

A potential workaround

The aim of radial distortion correction is to remove the long range (or large scale) distortion, since the curving of supposedly straight lines (e.g., building walls) is only really visible once the distortion produces a shift of more than one pixel. Unfortunately we cannot simply ignore the fractional pixel shifts --- this would be equivalent to using nearest-neighbour interpolation, with its associated artifacts.

Perhaps we can cheat a little: what if we pushed out interpolation coordinates away from a fractional pixel shift of 0.5? Let x' be the real-valued x component of our interpolation coordinate obtained from the radial distortion correction model above. Further, let x_f be the largest integer less than x' (the floor of x'). If x' - x_f < 0.5, then let d = x' - x_f. (We can deal with the d > 0.5 case by symmetry).

Now, if d > 0.375, we compress the value of d linearly such that 0.375 <= d' <= 0.425. We can obtain the new value of x', which we can call x", such that x" = x_f + (x' - x_f ) * 0.4 + 0.225. Looking back at Figure 3, we see that a fractional pixel shift of 0.425 seems to leave us with at least a little bit of contrast; this is where the magic numbers and thresholds were divined from.

Does this work? Well, Figure 7 shows the result of the above manipulation of the interpolation coordinates, followed by the same cubic interpolation method used in Figure 6.

Figure 7: The undistorted version of Figure 5. Resampling was performed using the modified interpolation coordinates followed by cubic interpolation. Rendered at 400% size with nearest-neighbour upscaling. (click for 100% view).

Careful squinting reveals that the additional fading patches observed in Figure 6 have been reduced noticeably. This looks promising. Of course, one might argue that I have just added some more aliasing to the image. Which might be the case.

Further testing will be necessary, especially on more natural looking scenes. I might be able to coax sufficient distortion from one of my lenses to perform some real-world experiments.

Further possibilities

Using the forced geometric error method proposed above, we can now extract at least some contrast at the frequencies near Nyquist. We also know what the fractional pixel shift was in both x and y, so we know what the worst-case loss-of-contrast would be. By combining these two bits of information we can sharpen the image adaptively, where the sharpening strength is adjusted according to the expected loss of contrast.

Stay tuned for part two, where I plan to investigate this further.

References

1. Fitzgibbon, A.W.: Simultaneous linear estimation of multiple view geometry and lens distortion. In: Proc. IEEE International Conference on Computer Vision and Pattern Recognition, pp. 125–132 (2001).
2. Thevenaz, P., Blu T. and Unser, M.: Interpolation revisited, IEEE Transactions on medical imaging, 19(7), pp. 39–758, 2000.